歴史を見渡すと、諸民族の興亡〔こうぼう〕や王朝の交代が頻繁で、人の世の移り変わりは諸行無常、定《さだ》めなきことが定めであるようにも見える。それでも歴史書を紐解《ひもと》き、国々の変遷をやや仔細《しさい》に見るならば、定めなき定めには、定めないなりの何か、定めとまでは言わずとも、類型や典型といったものがあることに、気づかざるをえない。

 国は興《おこ》り国は亡《ほろ》ぶ。その間２００年３００年、通常長くて５００年。歴史に名を残すほどの民族は大をなしてのち、一度傾《かたむ》きかけた国を再興させ大帝国を築いてから、やがて黄昏《たそがれ》の夕陽のごとく緩やかに傾いていく。

なぜ栄えた国が永続することなく傾いていくのかというのは、古来からの多くの史書の議論の的であって、これは当然歴史家に限らず、歴史に学んで自らの行く末を考えようとする万人の関心事である。

 

個々の事象の連鎖を超えた、国家興亡《こうぼう》の必然のダイナミクスが存在するのではないか、ということを初めて明快に論じたのは、１４世紀アラビアの史家、アブデルラフマーン・イブン・ハルドゥーンである。北アフリカの３−４世代ごとの頻繁な王朝交代劇を目にし、自らも政治家としてその過程にかかわったイブン・ハルドゥーンの歴史観は、国の物質的経済的盛衰《せいすい》と人々の連帯心、公共心、尚武《しょうぶ》の気風といった精神的資源が相関して時間差をともなって変動する、というもので、これはいまの我々が見ても非常に現代的なものである。

血みどろの内乱をくぐり抜けて一つとなった若く猛々《たけだけ》しい部族が、瞬《またた》く間に諸国を統一して大きな王国を築き上げる。支配者となった人々が数世代を経て、安逸《あんいつ》と奢侈《しゃし》の蜜に毒されていく。制度の整った国はそれでも拡大し、成功の分け前にあずかろうという人々の当然の希望は、妬《ねた》み嫉《そね》み派閥争いを生み、それは絶えざる支配層拡大圧力となる。人々は公共心や団結心（イブン・ハルドゥーンが「アサビーヤ」の名で呼んだもの）を失い国事に無関心となる。

 人々の身の回りの世話から始まって、宮廷の運営から戦《いくさ》まで、すべて辺境の民や異人たちの手に委《ゆだ》ねられるようになり、屋台骨《やたいぼね》のかしいだ家のように、国は内乱と外寇《がいこう》でやがて傾いてゆく。そして国は滅び、辺境の若々しい気風を持った異人たちの新しい国で置き換わり、歴史の新たなサイクルが始まる。

 

＊　＊　＊

 

時は流れ歴史は巡《めぐ》って２１世紀の初頭、イブン・ハルドゥーン史観の構造を現代的視点で再考しようとしたアメリカ人がいた。コネチカット大学の数理生物学者、ピーター・ターチン博士である。

人はなぜ国家を作るのだろうか。それは人が自由を求めるからである。孤立した個人を待つのは自由ではなく隷属である。なぜなら孤立した個人は自然環境、または団結した集団との争いに必ずや敗《やぶ》れるだろうから。自然環境や他の集団から自らの主権を守ることのできるほどに強く団結した集団のなかで、いかにして個人の自由を保障するのか、これこそが社会集団を構成する人間の永遠の課題である。

個人の内的精神的充溢《じゅういつ》と社会集団の量的物質的拡大との間の葛藤、そのなかにこそ国家の興隆と衰退のサイクルの謎を解く鍵があるのではないか。ターチン博士はこれを数理の枠組みに載《の》せることを考えた。彼はイブン・ハルドゥーンの描像をたった二つの量で表すという大胆な仮定をおこなった。人口もしくは領土面積、または国民総生産といった物質的尺度を数値で表現する「国力」と、自由の追求、団結心、公共心といった個々人の精神的資源に発する社会的凝集《ぎょうしゅう》力を数値で表した「アサビーヤ」とが、非線形連立微分《びぶん》方程式に従って相関発展するモデルを提案したのである。

 

 

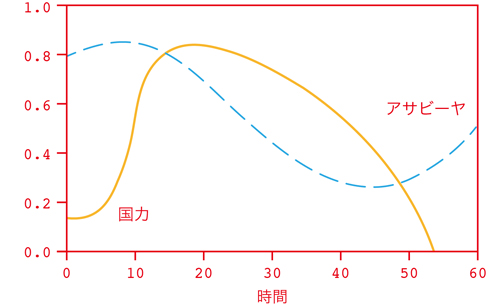
ターチン方程式の典型的な解。国力とアサビーヤの時間変化を表している。国家の興隆と滅亡がみられる。

驚くべきことにこの方程式は、国家が一度大発展をして滅ぶさまを記述していることを、ターチン博士は発見した。それは数理生物学者ターチンがこれまで扱ってきた、生物種の時間的発展をモデル化した「ロトカ＝ヴォルテラ方程式」には決してみられない性質であった。これは例えば草原にすむシマウマとライオンからなる生態系で、被食者シマウマの頭数と捕食者ライオンの頭数がどう変化するかを記述する方程式である。これを解くことで、両者がタイミングをずらしながら増減を繰り返す現実の様子が再現される。

 

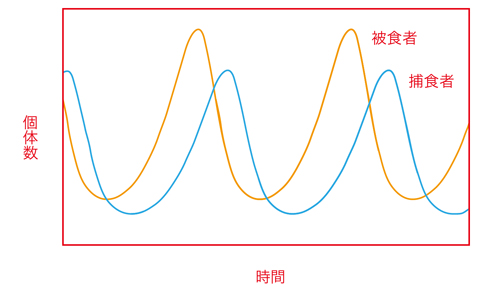
ロトカ＝ヴォルテラ方程式の解の一例

 

ターチン博士はこの方程式で発展するいくつかの国が地理的に隣接する状況を考えた。隣接国の大きさに十分な差ができた時点で、弱小国が強大国にある確率で吸収されると想定して、いくつかの地域の歴史上の国家分布から出発して、コンピュータ・シミュレーションをおこなってみた。すると実際の歴史の進行と似た発展パターンを得ることができたのである！　ここにその一例、唐からモンゴルに至る中国とその辺境の歴史を示してみる。

 

 

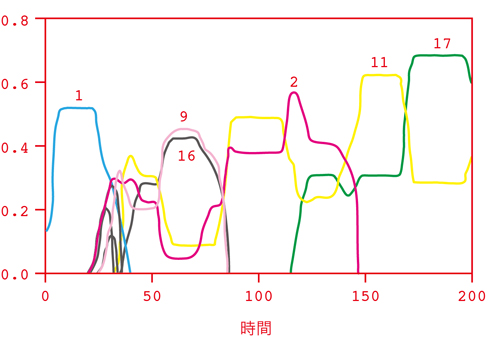
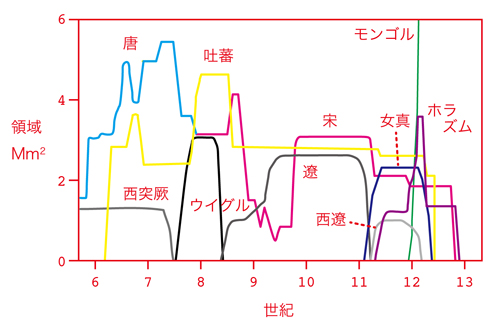
唐代から元代までの中国とその周辺の国家群の興亡のモデル。
左はターチン方程式に基づいたシミュレーションで、
右は歴史的データから推定再現したしたものである。
シミュレーション結果は、唐（1）宗（2）元（17）の交代継承と、
交代時の周辺国家の群生の様子を、
大略において捉えている。

多くのパラメータ・フィッティングをともなったこの結果自体を、どれほど真に受けるかは意見が分かれるだろう。しかしターチン博士のシミュレーションの対象は、この１例だけではなく、時代地域ともに多岐《たき》にわたるものである。それらの結果と歴史データとの統計的解析から、モデルの有効性がはっきりと示されていると、彼は考えている。

ターチン博士は自らの方程式の一般的有効性を実証するため、各国の歴史文献から組織的に定量的指標を抽出する作業を始めている。そこには人口、食料生産量、陶器の変遷や武具の変遷といった従来のハードな考古学的歴史的データにとどまらず、人名の変遷、文学の変遷の定量的指標といったソフトなものも含まれる。たとえば万葉の人麻呂の雄渾《ゆうこん》な歌には平安期の拡張的心性がよく看取《かんしゅ》され、新古今の定家の繊細なマニエリスムには私的逸楽《いつらく》を重視する鎌倉期の空気が読み取れるだろう。こうした歴史ビッグデータの蓄積は、ターチン方程式の検証にとどまらず、世界宗教の起源や伝搬についての定量的新研究という副産物を、すでに産み始めている。

 

歴史に関する言説を、微分方程式で表される「力学系」という定量的な記述の枠組みに載せさえすれば、あとはモデル化の精度の範囲内で定量的確定的な予言を得ることができて、その言説の真偽を歴史のデータに照らして判別することができる。それが可能な現代に、定性的な文献のみに基づいて、主張と対立主張の水掛け論のような歴史論戦を、いつまでも続けることができるだろうか。

数理的な歴史記述は、いまのところまだ素朴で図式的なもので、社会学者や歴史学者からすれば、現実の粗《あら》すぎる戯画《ぎが》にすぎないと思われるだろう。しかし一方、細菌の集団、動物の集団、さらには企業の集団の動力学を成功裏に記述する数理生物学的手法が、人間の集団にだけは決して適用されないと考えることは困難である。そしてこの戯画が頑強な数理的背骨を持つ事実は、この粗い描像にまだいくらでも健全な発展の余地があることを示唆《しさ》している。政体２つの競合を考えた４自由度系にどんなドラマが隠されているだろうか。３政体６自由度の織りなす三国志はどのようなものであろうか。

力学系理論の教科書を開いて目次を見れば、そこには「終着状態分岐」「安定状態と危機」「事象のカスケード」「カオス的奇妙な終着状態」といった文字が見つかる。あたかも我々のまわりの社会事象に関するかのようなこれら諸概念は、すべて厳密な数学的定義を持つ力学系理論の熟語なのである。自らが歴史事象の記述に適用されるのを、これら諸概念が今か今かと待っているさまを想像してみようではないか。

数理物理学的または数理生物学的な道具立てだけに依《よ》って、人間社会や歴史を研究することはもちろんできない。社会学や歴史学の研究には、今後もいままで通り、地道な文献収集作業と人間性の深い哲学的理解に裏打ちされた広範な教養とが前提になるだろう。しかしながら、数理生物学と複雑系科学の最近の進展を見るにつけ、社会学者や歴史家といえども、数学や物理学との無縁を、いつまでも決め込むわけにはいかないのではないか。

いやそうではない。きっと今世紀半ばには社会学や歴史学こそが、数学的言語と道具立てを自在に使いこなす人文科学の代表として、人間が過去に学んで同じ愚《ぐ》を何度も繰り返し続ける悲劇を避けるための定量的科学として、新世紀の人文学の先陣を切っているのではないか。筆者にはそのように思えるのだ。

ちょうど星々や銀河の波乱に満ちた一生を、天体物理学の方程式がわずか数行に封《ふう》ずることができるように、もしも民族や王国の興亡の秘密を、歴史力学の数行の方程式が語り始めるのだとするならば、それはとても魔術的な、心躍る物語であるに違いない。